The rectangle is one of the most important shapes in the world of maths which is the main reason that everyone should be clear about the basic properties and formulas associated with it. The figure of a rectangle is horizontal and two-dimensional. In an AB plane, if you need to represent a figure of the rectangle, arms, that represents length will be A-axis and the arms that represent width will be B-axis, respectively.
As you must be already aware subsequent are some common objects or things that we see in our daily lives and are the shape of a rectangle.
· Televisions
· Tennis Courts for playing
· Magazines you read
· Walls that surround us
· Mobile phones
· Most of the Tables
· Books and many others.

Moving on, take a look at some of the essential properties of a Rectangle:
- A rectangle is also recognized as a quadrilateral
- The edges that are opposite are equivalent and parallel.
- Every angle on the inside is equivalent to ninety degrees
- The inner angles are equal to 360 degrees
- The diagonals intersect between themselves
- The length of both diagonals is similar
- If the lengths on the sides of a rectangle are denoted as x and y. The calculation of the perimeter will be 2x+2y units
- If the lengths on the sides of a rectangle are denoted as x and y. The area would be calculated as XY sin 90 = XY square unit
- A rectangle’s diagonal is the diameter of its circumcircles
- Because it has four right angles, it is also known as a parallelogram
- The result of length and breadth of a rectangle is known as its area
- The intersection in diagonals amongst each other occurs at dissimilar angles. One is known as an acute angle, and another is known as obtuse angle
- If bisection of two diagonals amongst each other occurs at right angles, then the rectangle is known as square
- You get a cylinder if you rotate the rectangle along the line that joins the midpoint of parallel sides which are longer. In this situation, the cylinder’s height and the width of the rectangle are equal. Also, the diameter of the cylinder is equal to the rectangle’s length.
- You get a cylinder if you rotate a rectangle along the line that joins the midpoint of shorter parallel sides. In this situation, cylinders’ height and rectangles length are equal. Similarly, the diameter of the cylinder is equal to the rectangle’s width
The major difference between a rectangle and a square is that the sides of a rectangle that are opposite to each other are equal, whereas all the sides in a square are equal.
The rectangle is categorized by its length (L) and its breadth (W). The size of length and breadth differ.
Suppose we take a rectangle; with four sides as ABCD. The right angles on the interior would be A, B, C and D. The distance from angle A to B or angle C to D is defined as length (L), while the measurement between B to C or A to D is defined as breadth (W) of the rectangle.
Calculation of Rectangle’s Perimeter

The perimeter of rectangle is considered as the distance around the sides of the figure of rectangle, twice the length and breadth. The dimension is calculated unit length-wise. The formulation for calculating perimeter is given as follows:
(P) Perimeter = 2 (length of rectangle + width of rectangle)
Calculation of Rectangle’s Area
Always remember these three important steps for calculating Area:
Step 1: The data always offers dimensions of length and breadth, make a note of them
Step 2: Multiply the values of the length and the breadth
Step 3: The answer has to be calculated in square units
The area that is covered by the total product of the length and width of the rectangle is called its Area. Measurement is done in square units. Hence, the area is also known as the total of all the four sides.
To calculate the area of the rectangle we have to depend on sides. Essentially, the formula is calculated based on the result of the length and breadth of the rectangle. While, if we talk about the perimeter it is considered as the total of all four edges. Hereafter, the section surrounded by the perimeter is considered as an area of a rectangle.
Suppose, if some figures have three dimensions, the total and lateral areas of the surface can easily be calculated. But because a shape of rectangle only has two dimensions, it is not possible.
So, based on these details that we have, the calculation of the area of a rectangle is derived as follows:
Area (A) = length * breadth
(A) = lb
How to calculate the length of diagonals in a rectangle?
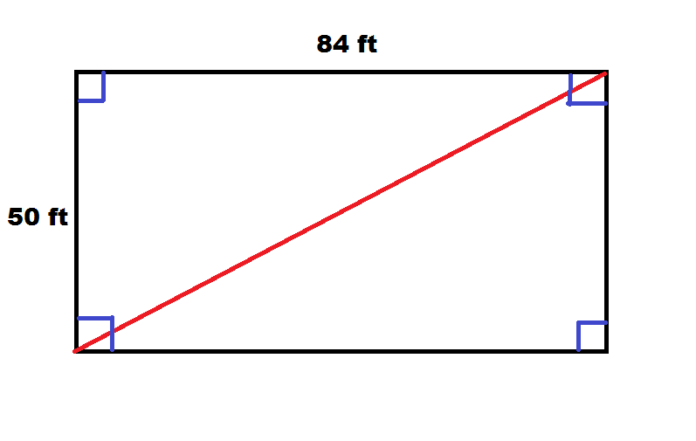
The figure of a rectangle as discussed is symmetrical and so both diagonals in a rectangle display equal length. After we divide the diagonals, as a result, we get two equal right-angled triangles. Therefore, the Pythagoras theorem can help us easily calculate the length of the diagonal where the diagonals are supposed as hypotenuse of right triangles.
Consider the hypotenuse as X, length as (L), and Breadth as (B) the perpendicular and the base, correspondingly. Hereafter, the length of the diagonal can be calculated as:
X=L2+B2−−−−−√
As is the case with all the chapters of mathematics, this chapter also requires a lot of practice, solving more problems gives you a deeper understanding of the subject matter. Cuemath explains and clears all your doubts; they have experts who deal with all your queries. You should definitely solve the worksheets they provide. The more you practice, the stronger your base becomes. Understanding the concepts clearly, helps you make use of them in solving various other problems from the course as well. You are sure to do well in the subject if you consider taking help from experts in the field. This will make it easier for you to solve the problems with ease.






